
如圖,,在△ABC中,,點(diǎn)D、E分別在AB,、AC邊上,,DE∥BC,若 AD:DB=1:2,AE=2,,則AC=( ),。
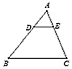


如圖,,在△ABC中,,點(diǎn)D、E分別在AB,、AC邊上,,DE∥BC,若 AD:DB=1:2,AE=2,,則AC=( ),。


6
相似三角形的性質(zhì)的定義
相似三角形性質(zhì)定理:
(1)相似三角形的對(duì)應(yīng)角相等。
(2)相似三角形的對(duì)應(yīng)邊成比例,。
(3)相似三角形的對(duì)應(yīng)高線的比,,對(duì)應(yīng)中線的比和對(duì)應(yīng)角平分線的比都等于相似比。
(4)相似三角形的周長(zhǎng)比等于相似比,。
(5)相似三角形的面積比等于相似比的平方,。
(6)相似三角形內(nèi)切圓、外接圓直徑比和周長(zhǎng)比都和相似比相同,,內(nèi)切圓,、外接圓面積比是相似比的平方
(7)若a/b =b/c,即b2=ac,,b叫做a,c的比例中項(xiàng)
(8)c/d=a/b 等同于ad=bc.
(9)不必是在同一平面內(nèi)的三角形里
①相似三角形對(duì)應(yīng)角相等,,對(duì)應(yīng)邊成比例.
②相似三角形對(duì)應(yīng)高的比,對(duì)應(yīng)中線的比和對(duì)應(yīng)角平分線的比都等于相似比.
③相似三角形周長(zhǎng)的比等于相似比
定理推論:
推論一:頂角或底角相等的兩個(gè)等腰三角形相似,。
推論二:腰和底對(duì)應(yīng)成比例的兩個(gè)等腰三角形相似,。
推論三:有一個(gè)銳角相等的兩個(gè)直角三角形相似。
推論四:直角三角形被斜邊上的高分成的兩個(gè)直角三角形和原三角形都相似,。
推論五:如果一個(gè)三角形的兩邊和其中一邊上的中線與另一個(gè)三角形的對(duì)應(yīng)部分成比例,,那么這兩個(gè)三角形相似。
推論六:如果一個(gè)三角形的兩邊和第三邊上的中線與另一個(gè)三角形的對(duì)應(yīng)部分成比例,,那么這兩個(gè)三角形相似,。
查看答案
單次付費(fèi)有效 3.99 元
用于查看答案,單次有效 19.99元
包月VIP 9.99 元
用于查看答案,,包月VIP無(wú)限次 49.99元